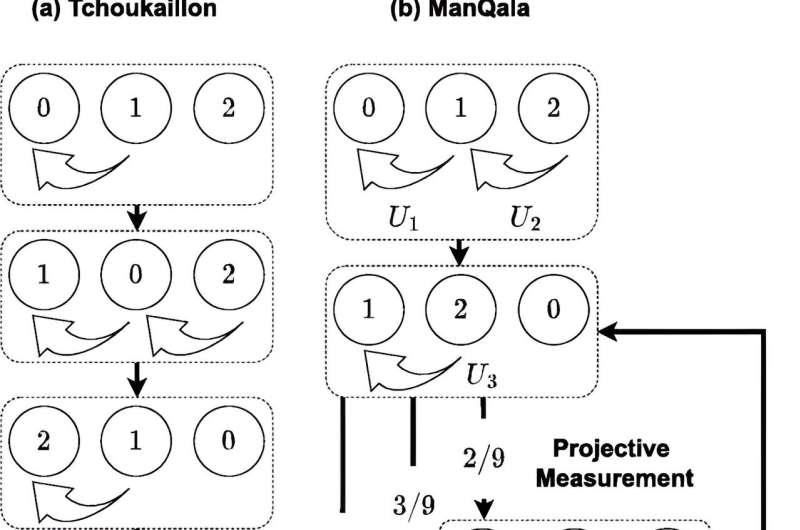
Beispielspielbretter für (a) Tchoukaillon (ein Solitär-Winkelmesser) und sein direktes quantitatives Gegenstück ManQala in (b). Hier zeigen wir beide Felder mit N = 3 Steinen und M = 3 Gitterstellen und stellen die Aussaat mit Pfeilen dar (die in der Winkelmesserstelle zu einheitlichen Operatoren werden). Sequentielle Einheitsverfahren1 Und du2 In der Abbildung ist das deterministische Quantenanalogon der ersten beiden Bewegungen eines Chockleons über Permutationen zwischen Ort und Population dargestellt. Der letzte Zug von Tchoukaillon hat in der Quantenversion des Spiels keine einheitliche hyperbolische Umsetzung. Daher Yu3 Führt den Fall an, in dem die Wahrscheinlichkeit, das Gewinnerbrett zu beobachten, maximiert ist. Bei der Beobachtung (projektive Messung) wird der Zielzustand erreicht, | 3,0,0⟩ mit einer Wahrscheinlichkeit von 4/9 und ein weiterer Fall, bei dem es sich um eine deterministische Aktion außerhalb des Zielfalls handelt, | 0,3,0⟩ wird mit einer Wahrscheinlichkeit von 2/9 (insgesamt 6/9) erreicht. Mit einer Wahrscheinlichkeit von 3/9 kehrt die Platine zur Konfiguration vor U zurück3, also | 1,2,0⟩ und der letzte Schritt wird wiederholt, bis er erfolgreich ist. Kredit: AVS Quantenwissenschaft (2023). doi: 10.1116/5.0148240
Winkelmesserspiel Es entstand vermutlich bereits 6000 v. Chr. in Jordanien Es wird bis heute auf der ganzen Welt gespielt. Es besteht aus Steinen, die die Spieler zwischen einer Reihe kleiner Löcher auf einem hölzernen Spielbrett bewegen. Ziel des Spiels ist es, alle Steine in das letzte Loch am Ende des Spielbretts zu bringen.
In einer neuen Studie veröffentlicht in AVS QuantenwissenschaftForscher der Tulane University haben eine modifizierte Solitärversion des Winkelmessers, die sie ManQala nennen, auf die Quantenzustandsgeometrie angewendet, das Gebiet der Quantenphysik, das sich mit der Überführung von Quantensystemen in bestimmte Zustände beschäftigt.
Das zentrale Problem, das die Quantenzustandstechnik zu lösen versucht, ist laut Ryan Glaser, Assistenzprofessor für Physik am College of Science and Engineering: „Was muss ich tun, um mein Quantensystem in den Zustand zu bringen, den ich möchte?“ Im Wesentlichen müssen Forscher herausfinden, wie man Teilchen dazu bringt, an bestimmten Orten zu bleiben oder bestimmte Energien zu haben, um sie zu untersuchen und Quantencomputer einzusetzen.
Bei Quantenteilchen ist das schwieriger als beispielsweise bei Steinen auf einer Winkelmesserplatte. „Quantendinge sind im Allgemeinen sehr empfindlich und schwer zu kontrollieren“, sagte Glaser. „Das System kann schnell zusammenbrechen und dazu führen, dass Sie jeden quantitativen Vorteil verlieren, den Sie haben oder haben möchten.“
Quantenphysiker haben bereits einige Möglichkeiten, diese Probleme zu lösen, aber die von den Forschern dieser Studie durchgeführten Simulationen zeigten, dass ManQala selbst auf einfacheren Systemen effizienter ist. „Selbst bei diesen vereinfachten Drei- und Drei-Loch-Systemen sehen wir bereits Vorteile“, sagte Glaser.
Die Studie sei eine von vielen auf dem Gebiet der Quantenspiele, sagte Glaser, die „effektiv gewöhnliche Spiele wie Sudoku, Dame oder Tic-Tac-Toe nimmt und die Regeln der Quantenphysik auf sie anwendet und interessante Dinge sieht, die passieren könnten.“ Wenn man es mit Quantenteilchen und nicht mit physischen Steinen zu tun hat, besteht die Möglichkeit, dass die Teilchen sich gegenseitig stören, wenn sie sich in benachbarten „Gruben“ befinden. Dies bedeutet, dass mehr Züge zur Verfügung stehen, und zumindest für Mancala „kann man das Spiel gewinnen, wenn man die quantitativen Regeln verwendet, was mit den klassischen Regeln nicht möglich wäre“, sagte Glaser.
Obwohl sich diese Studie auf Simulationen konzentrierte, ist Glaser hinsichtlich zukünftiger Anwendungen des Winkelmessers optimistisch. „Im Moment liegt es noch im Bereich der Theorie, aber ich denke, dass es experimentell auf jeden Fall machbar ist“, sagte Glaser. Er hofft, ManQala auf einem IBM Quantum-Cloud-Computer anwenden zu können, den er in der Vergangenheit zusammen mit seinen Forscherkollegen Thomas Searles von der University of Illinois in Chicago und Brian Kirby, Assistenzprofessor für Physik in Tulane, für Forschungszwecke verwendet hat.
Mehr Informationen:
Onur Danaci et al, ManQala: Spielinspirierte Strategien für Quantenzustandstechnik, AVS Quantenwissenschaft (2023). doi: 10.1116/5.0148240
das Zitat: Wie ein antikes Brettspiel bahnbrechende physikalische Entdeckungen erschließen könnte (2023, 14. August) Abgerufen am 14. August 2023 von https://phys.org/news/2023-08-08-ancient-board-game-cutting-edge -Physik. Programmiersprache
Dieses Dokument unterliegt dem Urheberrecht. Abgesehen von fairem Handel zum Zweck des privaten Studiums oder der Forschung darf kein Teil ohne schriftliche Genehmigung reproduziert werden. Der Inhalt dient ausschließlich Informationszwecken.

„Gamer. Unglückliche Twitter-Lehrer. Zombie-Pioniere. Internet-Fans. Hardcore-Denker.“






More Stories
Identische Dinosaurier-Fußabdrücke auf zwei Kontinenten entdeckt
Der Perseverance-Rover der NASA beginnt einen steilen Aufstieg zum Rand eines Vulkankraters auf dem Mars
Der Generalinspekteur der NASA veröffentlicht einen vernichtenden Bericht über Verzögerungen beim Start des SLS-Raumschiffprojekts